Moving average filter18. Dec '13

Introduction

In this assignment we'll attempt to improve design of a moving average filter. The circuit accepts 16 signed 11-bit fixed point numbers as input and produces the average of those numbers, which is also signed 11-bit fixed point number. In this case we are using 4:2 carry-save adders and one carry-lookahead adder, this means that we have to compute the sums in several stages:

  1. Sign-extension

  2. 16 inputs to 8 sums using 4x CSA-s

  3. 8 sums to 4 sums using 2x CSA-s

  4. 4 sums to 2 sums using 1x CSA-s

  5. Final sum using CLA

  6. Divide by 16

The last step, division by 16 is implemented by proper wiring. Division by power of 2 can simply be replaced with bit shift.

Show the design with sign extension

Assuming that input format is a signed 11-bit fixed point number with following sign bit, integer bit and fraction bit distribution:

4  3  2  1  0 -1 -2 -3 -4 -5 -6
S  I  I  I  I  F  F  F  F  F  F

Each carry-preserving CSA step adds one bit to the output. That could result in 15-bit number for the final sum. This means that we have to prepend 4-bits to each input with their corresponding sign bits:

14 13 12 11 10 9  8  7  6  5  4  3  2  1  0 (i)

E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •

E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •

E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •

E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
E  E  E  E  S  •  •  •  •  •  •  •  •  •  •
-------------------------------------------
S  •  •  •  •  •  •  •  •  •  •  •  •  •  •

Each sign extension could be represented as:

\begin{equation*} E_k = S_k \cdot \sum_{i=11}^{14} 2^i \end{equation*}

Knowing that we don't care about the overflowing carry bit we can rewrite that formula as:

\begin{equation*} E_k = \bar{S_k} \cdot 2^{11} + \sum_{i=11}^{14} 2^i \end{equation*}

In expaneded form:

\begin{equation*} E_k = \bar{S_k} \cdot 2^{11} + 2^{11} + 2^{12} + 2^{13} + 2^{14} \end{equation*}

Sum of 16 sign extensions yields:

\begin{equation*} E = \sum_{k=1}^{16} (\bar{S_k} \cdot 2^{11}) + 16 \times (2^{11} + 2^{12} + 2^{13} + 2^{14}) \end{equation*}

Multiplication by 16 can be substituted by shifting bits left by 4:

\begin{equation*} E = \sum_{k=1}^{16} (\bar{S_k} \cdot 2^{11}) + 2^{15} + 2^{16} + 2^{17} + 2^{18} \end{equation*}

Knowing that we don't care about bits on positions higher than 14, we can omit them:

\begin{equation*} E = \sum_{k=1}^{16} (\bar{S_k} \cdot 2^{11}) \end{equation*}

Thus we can rewrite our initial operands as following:

   14 13 12 11 10  9  8  7  6  5  4  3  2  1  0 (i)

            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •

            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •

            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •

            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
            !S  S  •  •  •  •  •  •  •  •  •  •
-----------------------------------------------
    S  •  •  •  •  •  •  •  •  •  •  •  •  •  •

Calculate minimum period for the clock using the proposed architecture

Latencies are assumed as followed:

  • Sign-extension is of one NAND gate: 2Δ

  • CSA: 4Δ

  • CLA: 8Δ

  • Division by 16: 0Δ

This results total delay of:

\begin{equation*} 2\Delta + 3 \times 4\Delta + 8\Delta = 22\Delta \end{equation*}

How to reduce this period?

Possible options include:

  • Overclocking of course

  • Tradeoff between area and latency, replace CSA's with something faster

  • Completely redesign the circuit

The last bullet point means that we get rid of the whole addition circuitry and just use one 2-operand adder and subtractor plus a register to hold previously calculated sum.

Implementation with 4:2 counters and CLA

We use 4:2 counter that works on bit vectors:

library ieee;
use ieee.std_logic_1164.all;

-- 15-bit 4:2 counter

entity counter42 is
    port ( a : in  STD_LOGIC_VECTOR (14 downto 0);
           b : in  STD_LOGIC_VECTOR (14 downto 0);
           c : in  STD_LOGIC_VECTOR (14 downto 0);
           d : in  STD_LOGIC_VECTOR (14 downto 0);
           s : out  STD_LOGIC_VECTOR (14 downto 0);
           co : out  STD_LOGIC_VECTOR (14 downto 0));
end counter42;

architecture behavioral of counter42 is

signal si : STD_LOGIC_VECTOR (14 downto 0);
signal ti : STD_LOGIC_VECTOR (15 downto 0);

begin

    ti(0) <= '0';
    counter_loop: for j in 0 to 14 generate
        -- First 3:2 counter
        si(j) <=  c(j) xor b(j) xor a(j);
        ti(j+1) <= (c(j) and b(j)) or ((b(j) xor c(j)) and a(j));

        -- Second 3:2 counter
        s(j) <= si(j) xor d(j) xor ti(j);
        co(j) <= (si(j) and d(j)) or ((si(j) xor d(j)) and ti(j));

    end generate;

end behavioral;

The compact carry lookahead adder:

library ieee;
use ieee.std_logic_1164.all;

-- 15-bit carry look-ahead adder
entity carry_lookahead_adder is
    port (
        a  : in  std_logic_vector (14 downto 0);
        b  : in  std_logic_vector (14 downto 0);
        ci : in  std_logic;
        s  : out std_logic_vector (14 downto 0);
        co : out std_logic
    );
end carry_lookahead_adder;

architecture behavioral of carry_lookahead_adder is
    signal t : std_logic_vector(14 DOWNTO 0);
    signal g : std_logic_vector(14 DOWNTO 0);
    signal p : std_logic_vector(14 DOWNTO 0);
    signal c : std_logic_vector(14 DOWNTO 1);
begin
    -- Product stage
    g <= a and b;
    p <= a or b;

    -- Sum stage
    t <= a xor b;

    -- Carry stage
    c(1) <= g(0) or (p(0) and ci);
    carry_loop: for i in 1 to 13 generate
        c(i+1) <= g(i) or (p(i) and c(i));
    end generate;

    co <= g(14) or (p(14) and c(14));
    s(0) <= t(0) xor ci;
    s(14 downto 1) <= t(14 downto 1) xor c(14 downto 1);
end behavioral;

The VHDL code which binds the 4:2 counters and CLA together:

library ieee;
use ieee.std_logic_1164.all;

entity moving_average_filter is
    port (
        sin  : in  std_logic_vector (10 downto 0);
        clk  : in  std_logic;
        sout : out std_logic_vector (10 downto 0);
        rst  : in  std_logic
    );
end moving_average_filter;

architecture behavioral of moving_average_filter is
    -- Registers
    type tregisters is array (0 to 15) of std_logic_vector(14 downto 0);
    signal r : tregisters;

    -- Padded input value
    signal first : std_logic_vector(14 downto 0);

    -- First stage
    signal s11 : std_logic_vector(14 downto 0);
    signal s12 : std_logic_vector(14 downto 0);
    signal s13 : std_logic_vector(14 downto 0);
    signal s14 : std_logic_vector(14 downto 0);
    signal c11 : std_logic_vector(14 downto 0);
    signal c12 : std_logic_vector(14 downto 0);
    signal c13 : std_logic_vector(14 downto 0);
    signal c14 : std_logic_vector(14 downto 0);

    -- Second stage
    signal s21 : std_logic_vector(14 downto 0);
    signal s22 : std_logic_vector(14 downto 0);
    signal c21 : std_logic_vector(14 downto 0);
    signal c22 : std_logic_vector(14 downto 0);
    signal s22s : std_logic_vector(14 downto 0);
    signal c21s : std_logic_vector(14 downto 0);
    signal c22s : std_logic_vector(14 downto 0);

    -- Third stage
    signal s3 : std_logic_vector(14 downto 0);
    signal c3 : std_logic_vector(14 downto 0);
    signal c3s : std_logic_vector(14 downto 0);

    -- Final sum
    signal s : std_logic_vector(14 downto 0);
    signal c : std_logic_vector(15 downto 0);

    component counter42 is
        Port ( a : in  std_logic_vector (14 downto 0);
               b : in  std_logic_vector (14 downto 0);
               c : in  std_logic_vector (14 downto 0);
               d : in  std_logic_vector (14 downto 0);
               s : out  std_logic_vector (14 downto 0);
               co : out  std_logic_vector (14 downto 0));
    end component;


    component carry_lookahead_adder is
        Port ( a : in  std_logic_vector (14 downto 0);
               b : in  std_logic_vector (14 downto 0);
               ci : in  std_logic;
               s : out  std_logic_vector (14 downto 0);
               co : out  std_logic);
    end component;


begin
    process (sin, clk)
    begin
        if rst = '1' then
            -- Reset register
            for i in 0 to 15 loop
                r(i) <= "000000000000000";
            end loop;
        elsif rising_edge(clk) then
            -- Shift operands
            for i in 15 downto 1 loop
                r(i) <= r(i-1);
            end loop;

            -- Store first operand
            r(0) <= first;
        end if;
    end process;

    -- Sign extension
    sign_extension_loop: for i in 14 downto 11 generate
        first(i) <= sin(10);
    end generate;

    -- Connect lower 11-bits
    input_loop: for i in 10 downto 0 generate
        first(i) <= sin(i);
    end generate;

    -- First stage
    stg11: counter42 port map(a=>first, b=>r( 0), c=>r( 1), d=>r( 2), s=>s11, co=>c11);
    stg12: counter42 port map(a=>r( 3), b=>r( 4), c=>r( 5), d=>r( 6), s=>s12, co=>c12);
    stg13: counter42 port map(a=>r( 7), b=>r( 8), c=>r( 9), d=>r(10), s=>s13, co=>c13);
    stg14: counter42 port map(a=>r(11), b=>r(12), c=>r(13), d=>r(14), s=>s14, co=>c14);

    -- Second stage: Sum shifted carries & sums
    stg21: counter42 port map(a=>s11, b=>s12, c=>s13, d=>s14, s => s21, co => c21);
    stg22: counter42 port map(a=>c11, b=>c12, c=>c13, d=>c14, s => s22, co => c22);
    s22s <= s22(13 downto 0) & "0";   -- s22 is shifted by 1
    c21s <= c21(13 downto 0) & "0";   -- c21 is shifted by 1
    c22s <= c22(12 downto 0) & "00";  -- c22 is shifted by 2

    -- Third stage
    stg3:  counter42 port map(a=>s21, b=>s22s, c=>c21s, d=>c22s, s=>s3, co => c3);
    c3s <= c3(13 downto 0) & "0";     -- c3 is shifted by 1

    -- Final addition
    stg4: carry_lookahead_adder port map(a=>s3, b=>c3s, ci=>'0', s=>s);

    -- Write output
    division_loop: for i in 10 downto 0 generate
        sout(i) <= s(i+4);
    end generate;

end Behavioral;

Clock to pad latencies with 4:2 counter and CLA approach on Xilinx Spartan 3E XC5500E:

------------+------------+------------------+--------+
            | clk (edge) |                  | Clock  |
Destination |   to PAD   |Internal Clock(s) | Phase  |
------------+------------+------------------+--------+
sout<0>     |   18.045(R)|clk_BUFGP         |   0.000|
sout<1>     |   19.570(R)|clk_BUFGP         |   0.000|
sout<2>     |   22.070(R)|clk_BUFGP         |   0.000|
sout<3>     |   22.590(R)|clk_BUFGP         |   0.000|
sout<4>     |   23.284(R)|clk_BUFGP         |   0.000|
sout<5>     |   23.491(R)|clk_BUFGP         |   0.000|
sout<6>     |   25.868(R)|clk_BUFGP         |   0.000|
sout<7>     |   26.537(R)|clk_BUFGP         |   0.000|
sout<8>     |   28.455(R)|clk_BUFGP         |   0.000|
sout<9>     |   28.867(R)|clk_BUFGP         |   0.000|
sout<10>    |   29.660(R)|clk_BUFGP         |   0.000|
------------+------------+------------------+--------+

Show the complete circuit for the new design

The period of following circuit is of two CLA-s and delays caused by the registers. It should be roughly twice faster than previous design and should consume also less area:

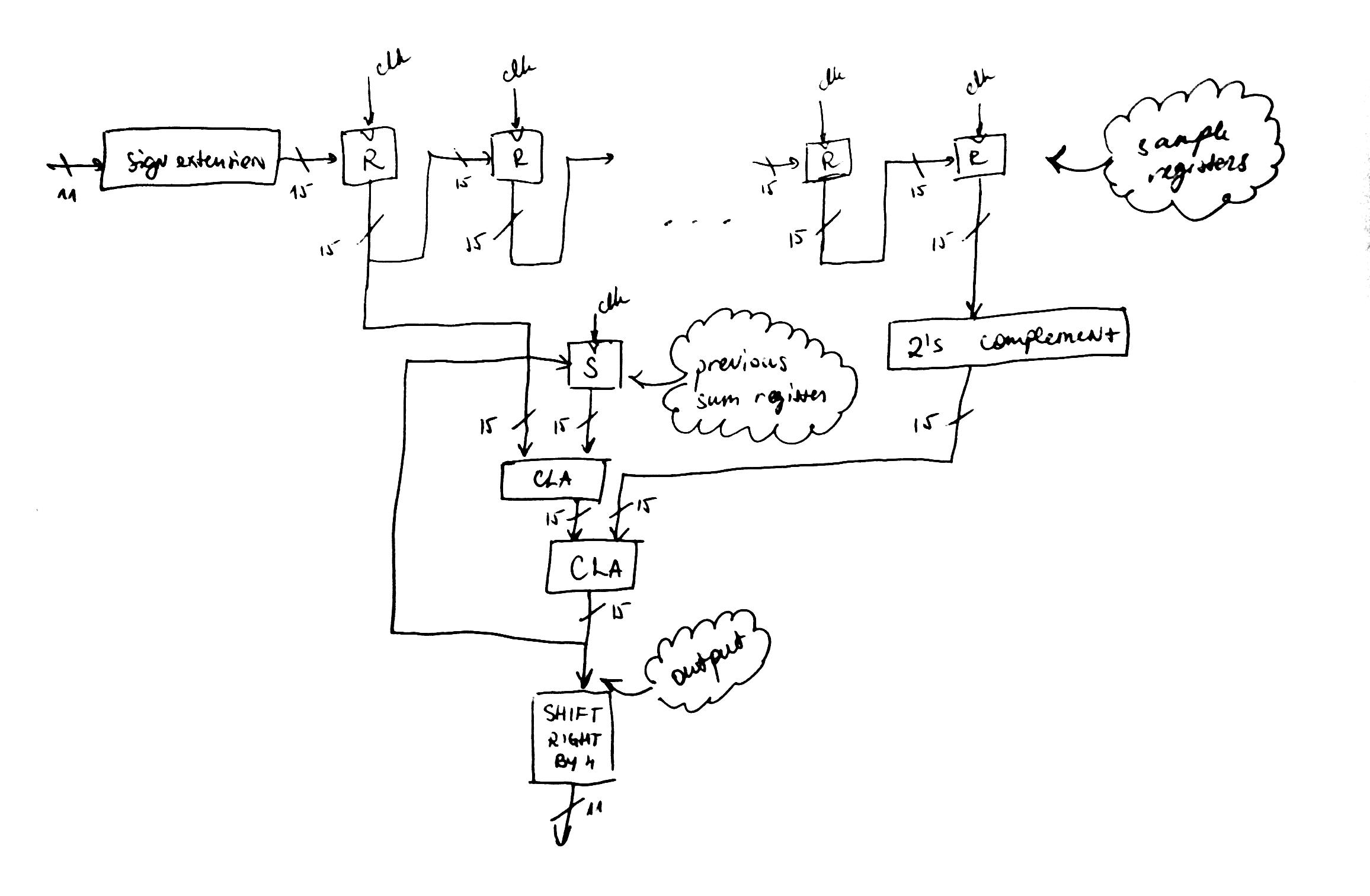
img/moving-average-filter-modified.png

Modified moving average filter

The implementation of new design

The improved design uses same carry lookahead adder but discards the 4:2 counters:

library ieee;
use ieee.std_logic_1164.all;

entity moving_average_filter is
    Port ( sin  : in  std_logic_vector (10 downto 0);
           clk  : in  std_logic;
           sout : out std_logic_vector (10 downto 0);
           rst  : in  std_logic);
end moving_average_filter;

architecture behavioral of moving_average_filter is
    -- Registers
    type tregisters is array (0 to 15) of std_logic_vector(14 downto 0);
    signal registers : tregisters;
    signal sum : std_logic_vector(14 downto 0);

    -- Wires
    signal addition              : std_logic_vector(14 downto 0);
    signal addition_carries      : std_logic_vector(14 downto 0);
    signal subtraction           : std_logic_vector(14 downto 0);
    signal subtraction_carries   : std_logic_vector(14 downto 0);
    signal first                 : std_logic_vector(14 downto 0);
    signal last                  : std_logic_vector(14 downto 0);

    component carry_lookahead_adder is
        Port ( a : in  std_logic_vector (14 downto 0);
               b : in  std_logic_vector (14 downto 0);
               ci : in  std_logic;
               s : out  std_logic_vector (14 downto 0);
               co : out  std_logic);
    end component;
begin
    process (sin, clk)
    begin
        if rst = '1' then
            -- Reset register
            for i in 0 to 15 loop
                registers(i) <= "000000000000000";
            end loop;
            sum <= "000000000000000";
        elsif rising_edge(clk) then
            -- Shift operands
            for i in 15 downto 1 loop
                registers(i) <= registers(i-1);
            end loop;

            -- Store first operand
            registers(0) <= first;

            -- Store sumious value
            sum <= subtraction;
        end if;
    end process;

    -- Sign extension
    sign_extension_loop: for i in 14 downto 11 generate
        first(i) <= sin(10);
    end generate;

    -- Connect lower 11-bits
    input_loop: for i in 10 downto 0 generate
        first(i) <= sin(i);
    end generate;

    -- Last operand
    last <= not (registers(15));

    -- Add first operand
    addition_stage: carry_lookahead_adder port map(a=>first, b=>sum, ci=>'0', s=>addition);

    -- Subtract last operand
    subtraction_stage: carry_lookahead_adder port map(a=>addition, b=>last, ci=>'1', s=>subtraction);

    -- Write output
    division_loop: for i in 10 downto 0 generate
        sout(i) <= subtraction(i+4);
    end generate;

end Behavioral;

Clock to pad latencies for Xilinx Spartan 3E XC5500E:

Clock clk to Pad
------------+------------+------------------+--------+
            | clk (edge) |                  | Clock  |
Destination |   to PAD   |Internal Clock(s) | Phase  |
------------+------------+------------------+--------+
sout<0>     |   12.472(R)|clk_BUFGP         |   0.000|
sout<1>     |   13.126(R)|clk_BUFGP         |   0.000|
sout<2>     |   13.671(R)|clk_BUFGP         |   0.000|
sout<3>     |   13.694(R)|clk_BUFGP         |   0.000|
sout<4>     |   14.166(R)|clk_BUFGP         |   0.000|
sout<5>     |   14.511(R)|clk_BUFGP         |   0.000|
sout<6>     |   14.705(R)|clk_BUFGP         |   0.000|
sout<7>     |   15.152(R)|clk_BUFGP         |   0.000|
sout<8>     |   15.132(R)|clk_BUFGP         |   0.000|
sout<9>     |   14.369(R)|clk_BUFGP         |   0.000|
sout<10>    |   14.614(R)|clk_BUFGP         |   0.000|
------------+------------+------------------+--------+

Analysis of the designs

The latency of 4:2 counter + CLA design is 29.66ns, which is three times better than the initial goal:

\begin{equation*} \frac{1}{29.66ns} \approx 34MHz \end{equation*}

The latency of adder-subtractor design has double the performance of previous design and it is nearly 7 times better than the initial goal:

\begin{equation*} \frac{1}{14.614} \approx 68MHz \end{equation*}

Adding a register to buffer the output would allow rising the frequency even higher, this would of course mean that the output would be delayed by one cycle.

Waveforms

The signal fed to the circuit:

\begin{equation*} S(t) = 10 cos ( 2 \Pi t \times \frac {10}{1000}) + sin(2 \Pi t \times \frac{100}{1000}) \end{equation*}

Yields in following charts for input and output:

Pygal-10-10-8-8-6-6-4-4-2-200224466881010
Conditional sum adder Carry ripple adder Carry look-ahead adder Hardware description languages Goldschmidt division implementation
computer arithmetic VHDL TU Berlin adder conditional sum adder